Machine learning for mapping groundwater salinity with well log data / A preliminary analysis in Lost Hills
This was presented as a poster at the AAPG Pacific & Rocky Mountain Joint Meeting (Las Vegas, October 2016). It is work in progress. Please do not cite.
Will Chang, Tule Analytics, wchang@gmail.com
David Shimabukuro, CSU Sacramento
Janice Gillespie, CSU Bakersfield
Michael Stephens, CSU Sacramento
Overview
Inferring groundwater salinity and lithology from oil well logs can be cast as an optimization problem, which can then be solved with a general machine learning tool such as Google’s Tensorflow. This approach results in code that is clear, concise, and easy to modify. The model behavior is easy to inspect, and the results are qualitatively correct.
An objective function for well log interpretation
Tensorflow finds local minima in a user-defined mathematical function \(f\). How do we construct \(f\) for well log interpretation?
1. The parameters of \(f\) are the quantities to be inferred. They are depth series vectors.
- Lithology \[ \begin{equation*} V_\textrm{shale}, V_\textrm{sand}, V_\textrm{water}, V_\textrm{oil}, V_\textrm{gas} \end{equation*} \]
- Fraction of fluid flushed \[ \begin{equation*} \pi_\textrm{i} \end{equation*} \]
- Salinity \[ \begin{equation*} \textrm{TDS} \end{equation*} \]
- Static SP \[ \begin{equation*} \textrm{SSP} \end{equation*} \]
2. Transform parameters for convenience
- Fluid volume \[ \begin{equation*} V_\textrm{fluid} = V_\textrm{water} + V_\textrm{oil} + V_\textrm{gas} \end{equation*} \]
- Sand porosity \[ \begin{equation*} \phi = \frac{V_\textrm{fluid}}{V_\textrm{sand} + V_\textrm{fluid}} \end{equation*} \]
- Water saturation \[ \begin{equation*} S_\textrm{w} = \frac{V_\textrm{water}}{V_\textrm{fluid}} \end{equation*} \]
- Water resistivity \[ \begin{equation*} R_\textrm{water} = \bigg(\frac{T\cdot \textrm{TDS}}{400000}\bigg)^{-0.88} \end{equation*} \]
3. Use petrophysical equations to compute predictions \(\hat\rho, \hat\phi_\textrm{n}, \hat R_\textrm{t}, \hat R_\textrm{i}, \widehat{\textrm{SP}}\). Account for clay-lined sand pores by setting Archie’s \(a < 1\). Account for distinct shale beds with the laminated sand/shale model.
- Formation density \[ \begin{equation*} \hat\rho = \rho_\textrm{shale} V_\textrm{shale} + \rho_\textrm{sand} V_\textrm{sand} + \rho_\textrm{water} V_\textrm{water} + \rho_\textrm{oil} V_\textrm{oil}. \end{equation*} \]
- Neutron porosity \[ \begin{equation*} \hat\phi_\textrm{n} = \phi_\textrm{n,shale} V_\textrm{shale} + \phi_\textrm{n,sand} V_\textrm{sand} + \phi_\textrm{n,water} V_\textrm{water} + \phi_\textrm{n,oil} V_\textrm{oil}. \end{equation*} \]
- Clean sand resistivity (Archie’s equation) \[ \begin{equation*} R_\textrm{t,clean} = \frac{a}{\phi^m \cdot S_w^n}R_\textrm{water} \end{equation*} \]
- Flushed sand resistivity (Archie’s equation) \[ \begin{equation*} R_\textrm{xo,clean} = \frac{a}{\phi^m \cdot S_w^n}R_\textrm{mf} \end{equation*} \]
- Invaded sand resistivity \[ \begin{equation*} R_\textrm{i,clean} = \bigg(\frac{\pi_i}{R_\textrm{xo,clean}} + \frac{1-\pi_i}{R_\textrm{t,clean}}\bigg)^{-1} \end{equation*} \]
- Deep resistivity (laminated sand/shale equation) \[ \begin{equation*} \hat R_\textrm{t} = \bigg(\frac{V_\textrm{shale}}{R_\textrm{shale}} + \frac{1 - V_\textrm{shale}}{R_\textrm{t,clean}}\bigg)^{-1} \end{equation*} \]
- Shallow resistivity (laminated sand/shale equation) \[ \begin{equation*} \hat R_\textrm{i} = \bigg(\frac{V_\textrm{shale}}{R_\textrm{shale}} + \frac{1 - V_\textrm{shale}}{R_\textrm{i,clean}}\bigg)^{-1} \end{equation*} \]
- SP deflection \[ \begin{equation*} \widehat{\textrm{SP}} = \textrm{SSP} + \frac{59 V_\textrm{shale} - 12 V_\textrm{water}}{V_\textrm{shale} + V_\textrm{water}} \bigg(\log_{10}\frac{R_\textrm{mf}}{R_\textrm{water}}\bigg) \end{equation*} \]
4. Compute terms, which compare predictions to actual measurements. Each is the sum of the squares of the errors, scaled by tuning parameters. Low is good.
- Density loss \[ \begin{equation*} \kappa_1\norm{\hat\rho - \rho}^2 \end{equation*} \]
- Neutron porosity loss \[ \begin{equation*} \kappa_2\norm{\hat\phi_\textrm{n} - \phi_\textrm{n}}^2 \end{equation*} \]
- Deep resistivity loss \[ \begin{equation*} \kappa_3\norm{\hat R_\textrm{t} - R_\textrm{t}}^2 \end{equation*} \]
- Shallow resistivity loss \[ \begin{equation*} \kappa_4\norm{\hat R_\textrm{i} - R_\textrm{i}}^2 \end{equation*} \]
- SP loss \[ \begin{equation*} \kappa_5\norm{\widehat{\textrm{SP}} - \textrm{SP}}^2 \end{equation*} \]
5. Compute terms, which indicate the plausibility of parameter settings. Low is good.
- Is salinity too extreme? \[ \begin{equation*} \kappa_6\norm{\log(\textrm{TDS}) - \log(10000)}^2 \end{equation*} \]
- Is salinity too unsmooth? \[ \begin{equation*} \kappa_7\norm{\Delta\Delta\log(\textrm{TDS})}^2 \end{equation*} \]
- Is SSP too unsmooth? \[ \begin{equation*} \kappa_8\norm{\Delta\Delta\textrm{SSP}}^2 \end{equation*} \]
6. Finally, sum loss terms and regularization terms to get \(f\).
Note: \(f\) has many hyperparameters. They are of three kinds:
- Well-specific: \(T\), \(R_\textrm{mf}\).
- Field-specific: \(a\), \(m\), and \(n\) in Archie’s equation; \(R_\textrm{clay}\); component densities \(\rho_\textrm{shale}\), \(\rho_\textrm{sand}\), \(\rho_\textrm{water}\), \(\rho_\textrm{oil}\); nphi responses \(\phi_\textrm{n,shale}\), \(\phi_\textrm{n,sand}\), \(\phi_\textrm{n,water}\), \(\phi_\textrm{n,oil}\).
- Model-specific: \(\kappa_1, \ldots, \kappa_8\).
Setting hyperparameters by optimizing against \(f\) generally does not work. They should be set by direct measurement or separate analyses, or by a general hyperparameter optimization method if enough ground-truth salinity data is available.
Tensorflow code corresponds closely to a model’s mathematical description.
The Python script well.py contains most of the code for the well log analysis shown below.
import numpy as np
import tensorflow as tf
from tensorflow import log, exp, square
from tensorflow import reduce_sum as sum
import util
def analyze():
########################## 0. well data and field parameters ##############
# load well-specific data
N, DEPTH, T, log_R_mf, log_R_t, log_R_i, rho, nphi, SP = util.read_well()
# density and nphi of clay, sand, water, oil, gas
rho_all = tf.constant([2.4 , 2.65, 1.0, 0.9, 0.0])
nphi_all = tf.constant([0.35, 0.0 , 1.0, 1.0, 0.0])
# resistivity of clay (with bound water)
R_clay = 8.0
# Archie's equation parameters
a_Arch, m_Arch, n_Arch = 0.8, 2.1, 3.0
########################## 1. declare parameters ##########################
# water salinity
log_tds = cubic_spline_variable(N, 100, log(10000.))
# lithology
V = tf.nn.softmax(tf.Variable(tf.zeros([N, 5]))) # N by 5 matrix
V_clay, V_sand, V_water, V_oil, V_gas = tf.unpack(V, axis=1) # columns of V
# fraction invaded
pi_i = tf.sigmoid(tf.Variable(tf.zeros([N])))
# static SP
SSP = cubic_spline_variable(N, 100, SP[N/2], scale=0.1)
########################## 2. transform parameters ########################
# water resistivity
log_R_water = -0.88 * (log(T / 400000.) + log_tds)
# derived lithological parameters
V_fluid = V_water + V_oil + V_gas
log_S_water = log(V_water / V_fluid)
log_phi = log(V_fluid / (V_fluid + V_sand))
########################## 3. petrophysical equations #####################
# predict density and neutron porosity
rho_pred = sum(V * rho_all, 1)
nphi_pred = sum(V * nphi_all, 1)
# predict deep resistivity
C_sand = exp(-(log_R_water - m_Arch*log_phi - n_Arch*log_S_water)) / a_Arch
C_t = V_clay / R_clay + (1 - V_clay) * C_sand
log_R_t_pred = -log(C_t)
# predict shallow resistivity
C_sand_mf = exp(-(log_R_mf - m_Arch * log_phi)) / a_Arch
C_i = V_clay / R_clay + (1-V_clay) * (pi_i * C_sand_mf + (1-pi_i) * C_sand)
log_R_i_pred = -log(C_i)
# predict SP
SP_deflect = (59 * V_clay - 12 * V_water) / (V_water + V_clay + 0.0001)
SP_temp_adjust = (T + 459.67) / (75 + 459.67)
SP_resistivity_adjust = (log_R_mf - log_R_water) / log(10.0)
SP_pred = SSP + SP_deflect * SP_temp_adjust * SP_resistivity_adjust
########################## 4. loss ########################################
loss = ( sum(square(log_R_t_pred - log_R_t))
+ sum(square(log_R_i_pred - log_R_i))
+ sum(square(rho_pred - rho )) * 5.
+ sum(square(nphi_pred - nphi )) * 3.
+ sum(square(SP_pred - SP )) * 1e-3 )
########################## 5. regularization ##############################
SSP_d = SSP[1:N] - SSP[0:N-1] # 1st derivative
SSP_dd = SSP_d[1:N-1] - SSP_d[0:N-2] # 2nd derivative
log_tds_d = log_tds[1:N] - log_tds[0:N-1] # 1st derivative
log_tds_dd = log_tds_d[1:N-1] - log_tds_d[0:N-2] # 2nd derivative
reg = ( sum(square(SSP_dd)) * 1e5
+ sum(square(log_tds_dd)) * 3e7
+ sum(square(log_tds - log(10000.)) * 1e-1)
+ sum(tf.nn.softplus(log_phi - log(0.7))) * 1.)
########################## 6. declare f and optimize ######################
f = loss + reg
# set up optimization
train_f = tf.train.AdamOptimizer(0.1, 0.9, 0.999).minimize(f)
sess = tf.Session()
sess.run(tf.initialize_all_variables())
# iterate
for i in range(1000):
sess.run(train_f)
if i % 100 == 99: print sess.run(f)
# write out results
names = 'N DEPTH T log_R_mf log_R_t log_R_i rho nphi SP ' \
+ 'log_R_t_pred log_R_i_pred rho_pred nphi_pred SP_pred ' \
+ 'rho_all nphi_all R_clay a_Arch m_Arch n_Arch ' \
+ 'log_tds log_R_water pi_i SSP V_clay V_sand V_water V_oil V_gas'
util.dump_results(names.split(), locals(), sess)
def cubic_spline_variable(N, M, init, scale = 1.):
# For vector parameters that represent smooth curves, optimization is
# faster when they are reparameterized as cubic splines, which have
# much lower dimensionality. For example, a 1000-element vector with
# a spline knot every 100 elements is reparameterized as 22 scalars.
t = np.arange(M) / float(M) # [0, 1)
b0 = (-2 * t + 3) * t * t # right height
b1 = 1 - b0 # left height
b2 = (t - 1) * t * t # right slope
b3 = ((t - 2) * t + 1) * t # left slope
bases = tf.constant(np.vstack((b0, b1, b2, b3)), dtype=tf.float32)
K = ((N-1) / M) + 1 # number of segments
x0 = tf.Variable(tf.fill([K+1], scale * init)) # heights
x1 = tf.Variable(tf.zeros([K+1])) # slopes
params = tf.pack([x0[1:K+1], x0[0:K], x1[1:K+1], x1[0:K]])
spline = tf.reshape(tf.matmul(params, bases, transpose_a=True), [-1])
return spline[0:N] / scale
analyze() # run programThis script runs in 10 seconds to produce the following analysis.
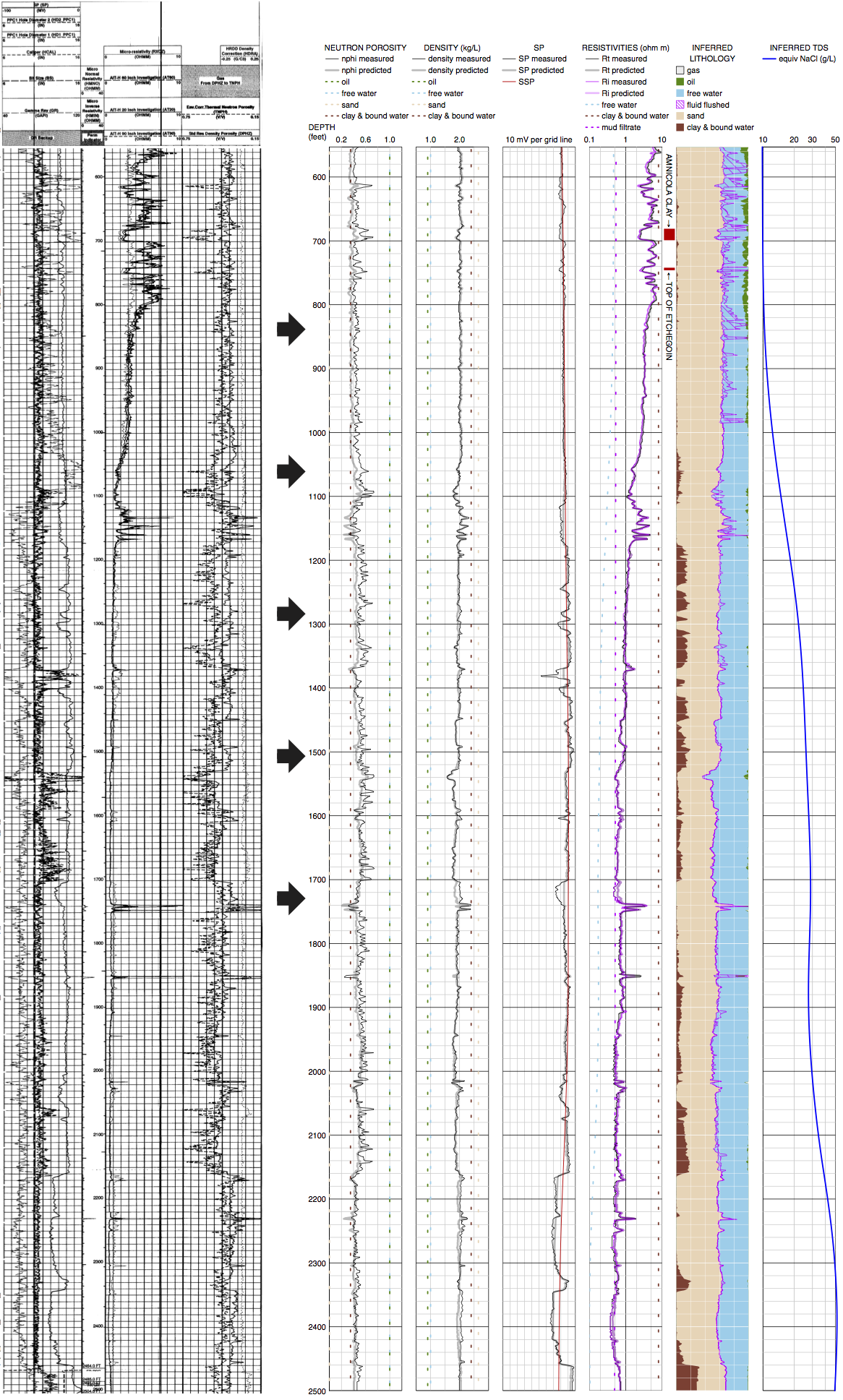
\(\triangledown\) Well \(\alpha\) from Lost Hills map view (API #03045353, Chevron WD7-1B, 2011). [Click image for PDF.]
An analysis in Lost Hills Oil Field
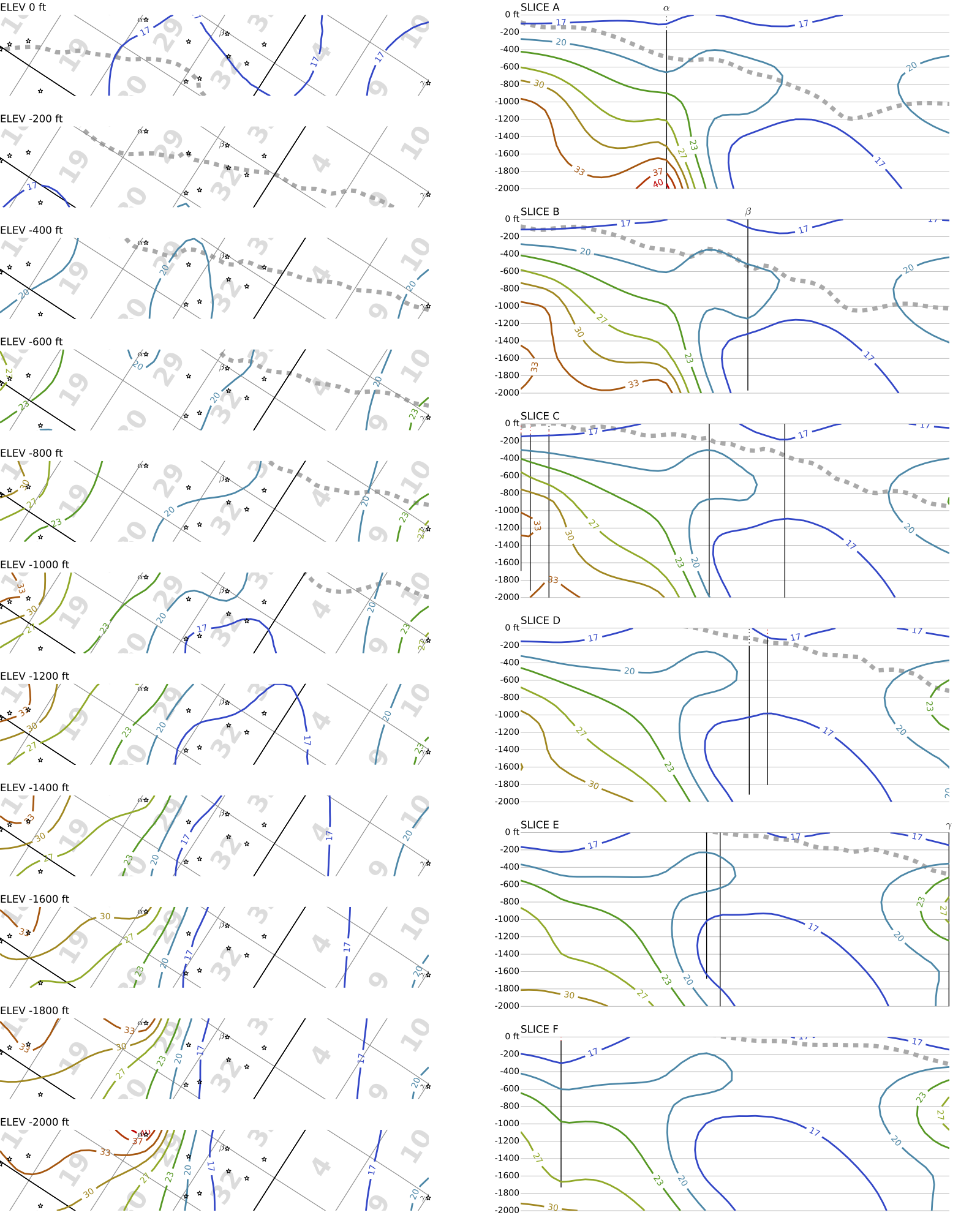
We can model volumes by parameterizing groundwater salinity as a 3D tensor and constraining nearby wells to have similar salinities. Below is a preliminary analysis of a box volume in the Lost Hills Oil Field.
\(\triangledown\) Map view, showing the volume of analysis with vertical slices (blue) and 13 wells (stars). The analyses for wells labeled \(\beta\) and \(\gamma\) are shown to the right. [Click image to enlarge.]
\(\triangledown\) Side view, showing the volume of analysis with horizontal slices (blue). Wells are drawn as vertical lines, showing which parts are unlogged (black dotted), logged but likely affected by steam (red dotted), and logged but probably cool (black solid). Only the lattermost are analyzed. [Click image to enlarge.]
\(\triangledown\) Horizontal slices (left) and vertical slices (right) showing groundwater salinity (color contours, g/L) and the Tulare/Etchegoin unconformity (gray dashed line, Tulare always closer to the top of this poster). Wells are projected onto the nearest vertical slice. [Click image to enlarge.]
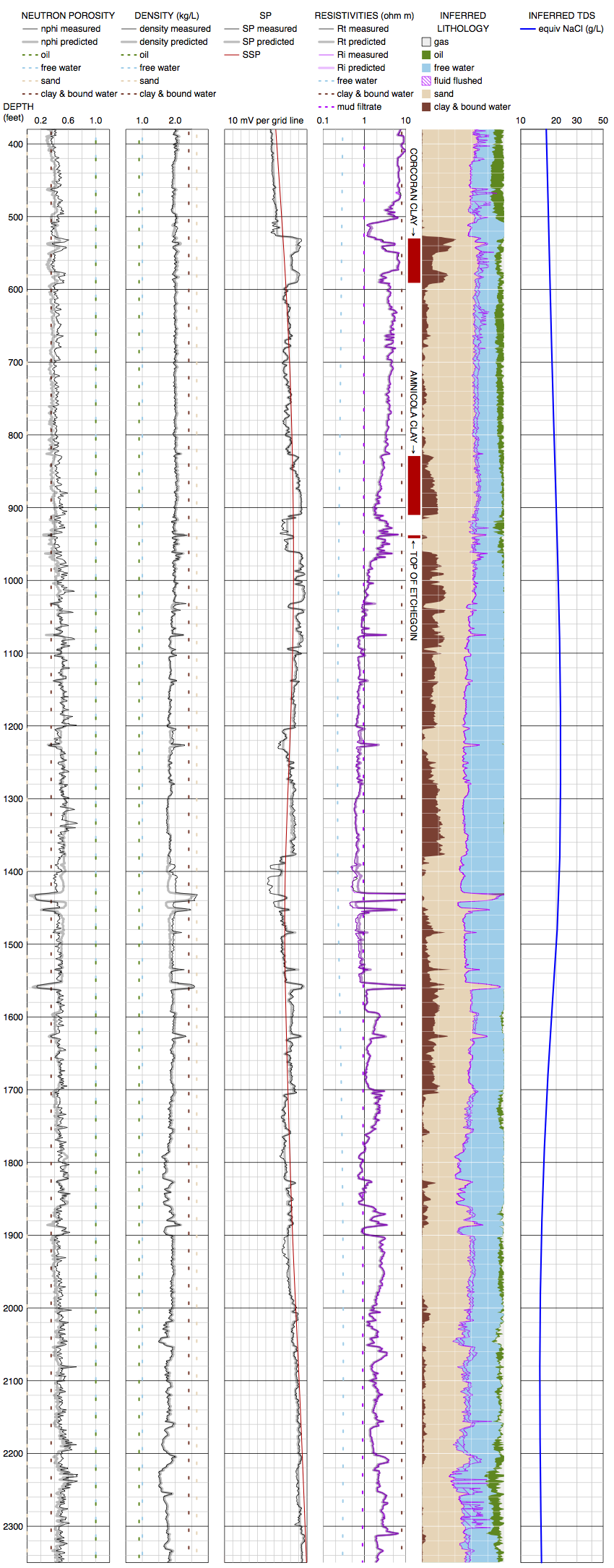
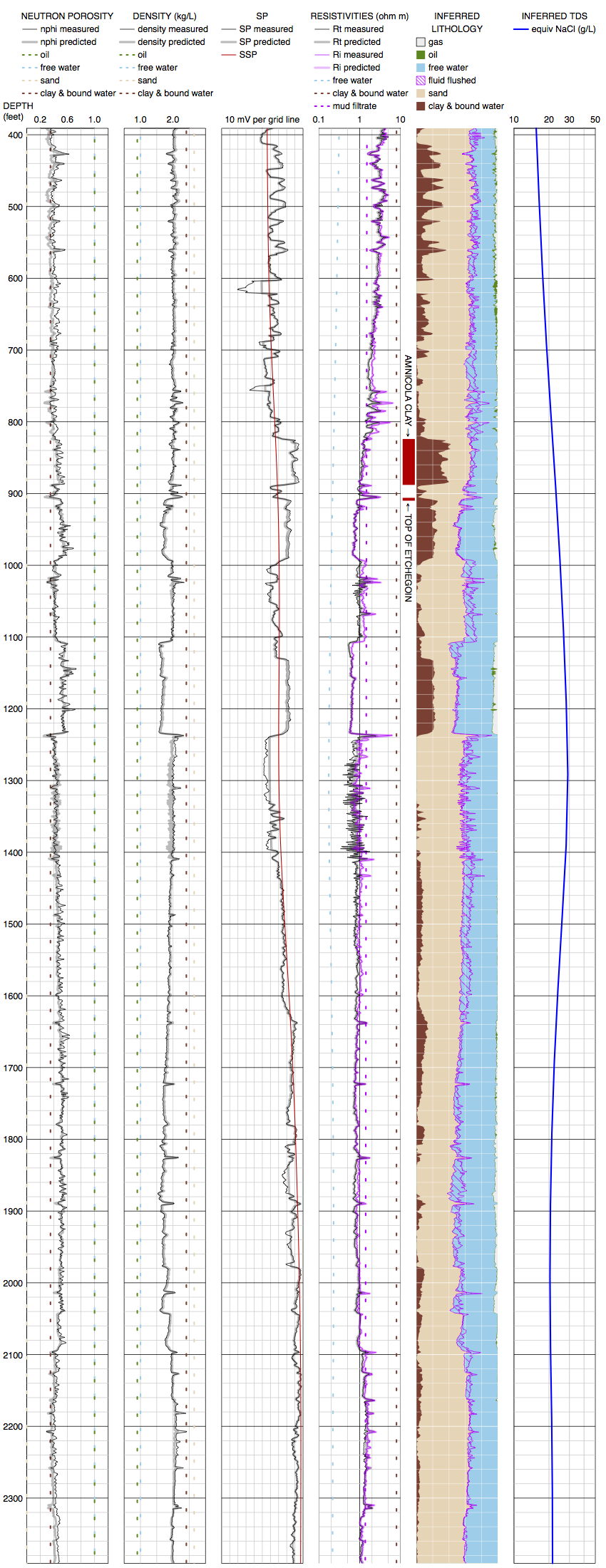
Mystery wells
The salinity trends for some wells in the volume analysis decreased with depth over some intervals. The full analysis for two such wells are shown here. Could this be real, or is this an artifact of steaming?
\(\triangledown\) Well \(\beta\) (API #03035136, Chevron 14-20UW, 2008) [Click image for PDF]
\(\triangledown\) Well \(\gamma\) (API #03007194, Chevron 11-1A, 1997) [Click image for PDF]
Discussion and future work
This method is essentially a synthesis of well-known methods for inferring groundwater salinity [1].
- Like the SP method, it uses the size of SP deflections as an indicator of \(\log(R_\textrm{water}/R_\textrm{mf})\).
- Like the resistivity-porosity method, it uses Archie’s equation to derive salinity from deep resistivity and porosity.
- Shallow resistivity is less probative, since the diatomite formations of Lost Hills can be impermeable to invading mud filtrate. However, the gap between deep and shallow resistivity still gives a useful lower bound on salinity.
Traditional methods work only in clean, wet sand. This model is robust in shale and hydrocarbon zones, since it can use extra variables (\(V_\textrm{shale}\), \(R_\textrm{shale}\), \(S_\textrm{water}\), etc.) to explain the movements of resisitivity and SP in these zones, while a smoothness constraint causes salinity to be interpolated over these zones.
This method can be elaborated in many ways.
- It can be augmented to handle other well log measurements such as gamma ray logging.
- It can be fitted with more realistic petrophysical equations, such as a dual water model for shaly sands.
- It can be made to acount for geologic formations, with abrupt changes in parameters allowed at formation boundaries.
These work items all involve introducing more hyperparameters into a model that already has many. Therefore, the highest priority for future work is to develop practical ways to set hyperparameters, along with validating the model in different oil fields against core analyses, mud logs, and geochemical measurements.
[1]: Lyle, Richard. 1988. Survey of the methods to determine total dissolved solids concentrations. U.S. Environmental Protection Agency Underground Injection Control Program.